UmiQS' Blog
0%

合并石子与哈夫曼树

发表于 分类于 ， Valine：

1. 合并石子题目分析

P1090 合并石子题目描述

根据题意，每次合并的代价为两堆石子的总重量之和。对于初始的一个石堆 $h$ ，只要它开始参与合并成一个新的石堆 $h’$ ，那么以后每次 $h’$ 在参与合并成为新堆的时候，总会有 $h$ 的代价计算在内。所以，一个原始石堆的代价可能会经过多次计算。那么，一个优化的方向就呼之欲出：使参与合并次数越多的石堆的重量越小。

2. 哈夫曼树（Huffman Tree）简介

2.1. 哈夫曼编码（Huffman Code）与合并石子

Huffman 树的一个重要运用是最小化变长编码的码平均长度：设有信源

编码后的码字分别为 $W_1$ , $W_2$ , $\cdots$ , $W_q$ ，各码字对应的码长度为 $l_1$ , $l_2$ , $\cdots$ , $l_q$ 。由于这是唯一可译码，信源符号 $s_i$ 和码字 $W_i$ 一一对应，则平均的编码长度为

如果把 $p(s_i)$ 看作编码树（二进制编码，是二叉树）的叶子节点的权值， $l_i$ 看作叶子节点的深度（定义根节点的深度为 0），那么上式所求的其实是该编码树的叶节点的带权平均深度。所以，Huffman 编码的优化方向等价于使叶节点的带权平均深度最小，换而言之，要使得码长度越长的信源符号出现的概率越小。

2.2. 哈夫曼树与合并石子的过程

合并石子的过程，可以绘制成为一棵二叉树。设有重量分别为 $a$ , $b$ , $c$ 的三个石堆，合并过程如下。

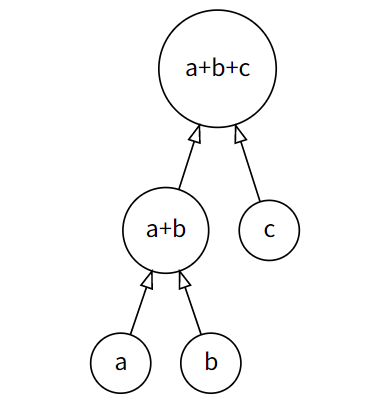
image-20210115081148079

由此得到的总代价为 $cost = (a+b)+(a+b+c) = 2a+2b+c$ 。若令 $p(s_1)=a$ , $p(s_2)=b$ , $p(s_2)=c$ 且 $l_1=depth(s_1)=2$ , $l_2=depth(s_2)=2$ , $l_3=depth(s_3)=1$ ，则有 $cost=\sum\limits_{i=1}^{3} p\left(s_{i}\right) l_{i}$ ，形式上与求二叉树的叶节点带权平均深度、信源编码的平均编码长度均相同。

所以，可以将合并石子的问题看作为 Huffman 编码的问题，每一个信源概率在数值上等于一个原始石堆的重量，每一个码字的长度在数值上等于一个原始石堆在总代价中参与计算的次数。

下面进行举例说明。设一开始有一对重量为 1、5、5、6 的石子，下图给出了一种最优解。

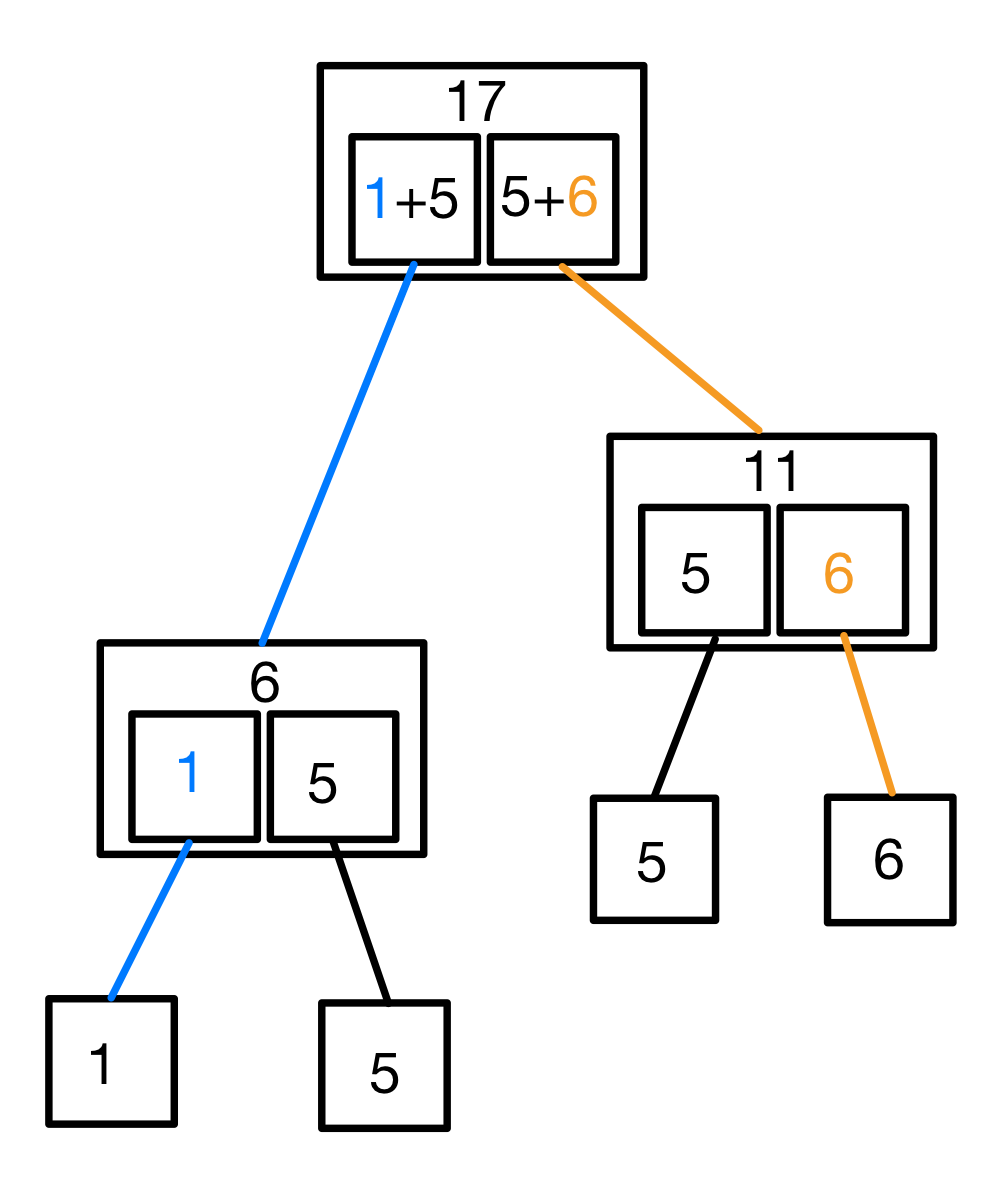
image-20210114195230706

以重量为 1 和 6 的石堆为例，同时，1 和 6 也可以视作叶子节点的权值。蓝色字体表示重量为 1 的石堆参与计算的那一部分；橙色字体表示重量为 6 的石堆参与计算的那一部分。观察可以发现，这也是一棵 Huffman 树。蓝色线条表示权值为 1 的叶节点的深度；橙色线条表示权值为 6 的叶节点的深度。可以看出，对于每个叶节点，参与计算的次数在数值上等于叶节点的深度。综上所述，合并石子问题与 Huffman 编码问题在数学上等价。

3. 合并石子的代码实现

与 Huffman 树的构造过程一模一样，只不过少了建树的过程。使用堆来维护整个序列，每次从堆顶连续取出两个元素，将两者的代价和计入总代价之中，直至最后堆中只剩下一个元素（该点也是 Huffman 树的根节点）。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
typedef long long LL;
int n;
LL ans = 0;

priority_queue<LL, vector<LL>, greater<LL> > q; //小根堆

int main()
{
   int i, j, x, y;
   scanf("%d", &n);
   for(i=1; i<=n; i++)
   {
       scanf("%d", &x);
       q.push((LL)x);
   }
   while(q.size() >= 2)
   {
       x = q.top(); q.pop();
       y = q.top(); q.pop();
       q.push((LL)(x+y));
       ans += (x+y);
   }
   printf("%lld", ans);
   return 0;
}

4. 合并石子的扩展

  • P1334 瑞瑞的木板：合并石子的逆向操作，代码与上面完全一样。题目由合并个体变为了切割整体，作图发现其本质与合并石子一样。