本文是自动控制原理课程中部分知识点的个人总结以及知识点的大纲罗列,并不是完整的原理公式汇总。
文中提到的教材是高飞、袁运能、杨晨阳所著的《自动控制原理》,所有章节和页码均对应于该教材上的内容。
所写的内容并不能完全反映该课程的所有知识点,请务必注意。
传递函数

第二章 时域分析
1. 典型输入
一阶系统
瞬态性能指标
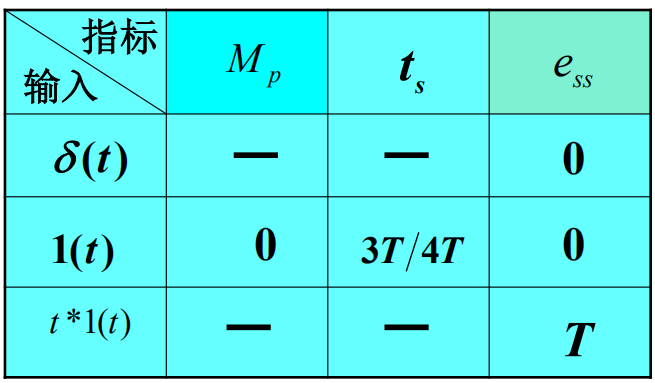
表达式
线性定常系统对输入信号导数(积分)的响应,等于系统对该输入信号响应的导数(积分)。
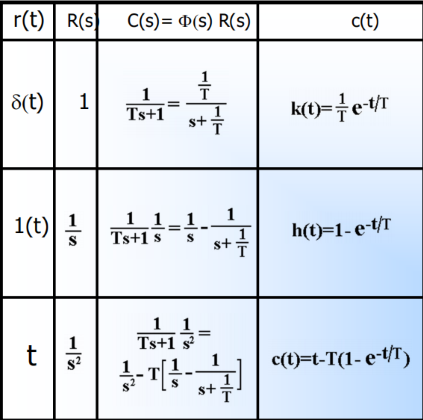
二阶系统:看教材即可,教材上的公式总结得够用了。
瞬态响应指标(重点是二阶系统)

高阶系统

2. 稳定性判断
系统稳定的充要条件:系统的特征方程的所有根都具有负实部,或者说都位于s平面的虚轴之左。
劳斯判据
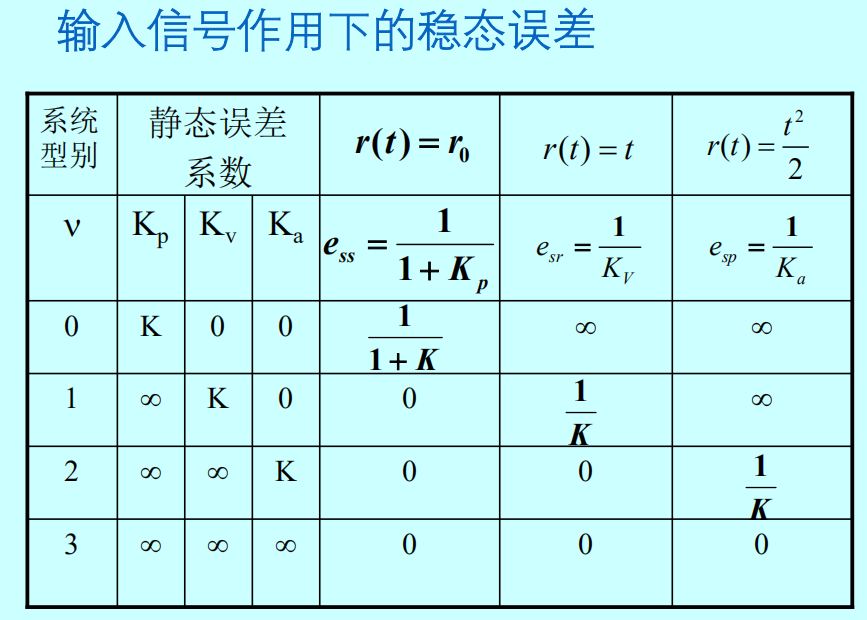
稳态误差分析
系统的型别
简单来说,就是$G(s)H(s)$中$\frac{1}{s}$因子的次数。

稳态误差表:见书P43~P44
第三章 根轨迹法
1. 根轨迹及其方程
2. 绘制根轨迹图
关于渐近线:
终点为无穷远的轨迹:渐近线
P58有常见的根轨迹渐近线的图示,随着$n-m$变化。
终点为开环零点的轨迹:终止角
3. 根轨迹分析
由开环零极点得到的是闭环特征根的轨迹特性。
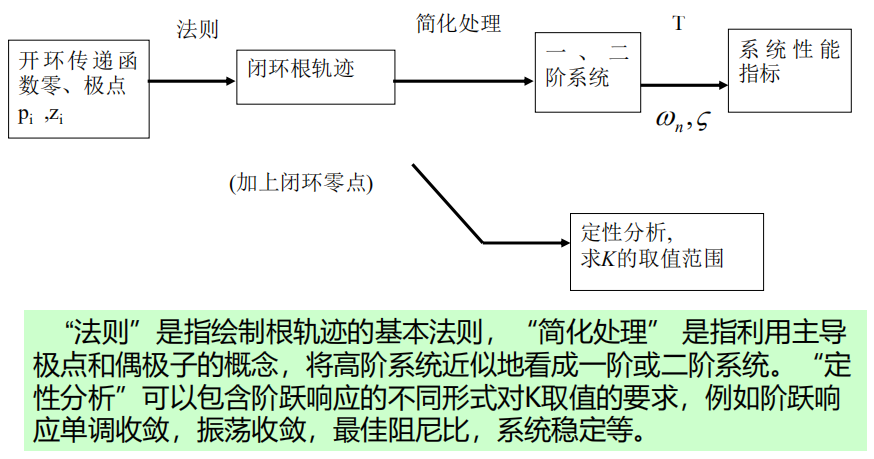
4. 绘制根轨迹模板(⭐️️)
由题可知极点$p$、零点$z$,并确定$n$、$m$,可以得到$n-m$
在坐标上画出零极点$p$、$z$
- 注意分析实轴上的零极点,确定实轴上的轨迹段(重根的个数要全都算上)。
- 估计轨迹图的大致走向,以及哪里会有分离点和会合点,渐近线可以由$n-m$来估计。这一步的作用是做到心中有数,根轨迹该知识什么样的。如果之后计算出现问题,有时候能够利用这个大致的印象发现错误。
计算会合/分离点$d$
- 重根要都算
- 如果有要求,看一下分离角和会合角。简单的轨迹图没啥好算的。
可以考虑渐近线:参考教材P58图3-6
计算与虚轴的交点(实轴的看题目要求)
法一:使用系统特征多项式
法二:劳斯判据
零极点在非坐标轴的情况下
- 极点:考虑起始角
- 零点:考虑终止角
- 在坐标轴上的一般能直接看出来
系统稳定性分析:和“计算与虚轴的交点”相结合
很难说哪个方法更好。使用系统特征多项式的方法更为直接,但是有时候会涉及高次(大于二次)方程的求解。使用劳斯判据计算$s$相对容易,但是最后也有一个带入求解的过程。两种具体的计算方法请参考教材。
第四章 频域分析
1. 典型环节频率特性:奈奎斯特曲线、波特图
注意:截止频率用分段函数比较好算,将在本章的技巧部分介绍。不要直接用$L(\omega)$,不然很可能出现超越方程。(二分法逼近警告)
2. 开环系统的频率特性
3. 奈奎斯特稳定判据(频域稳定判据)
注意事项:
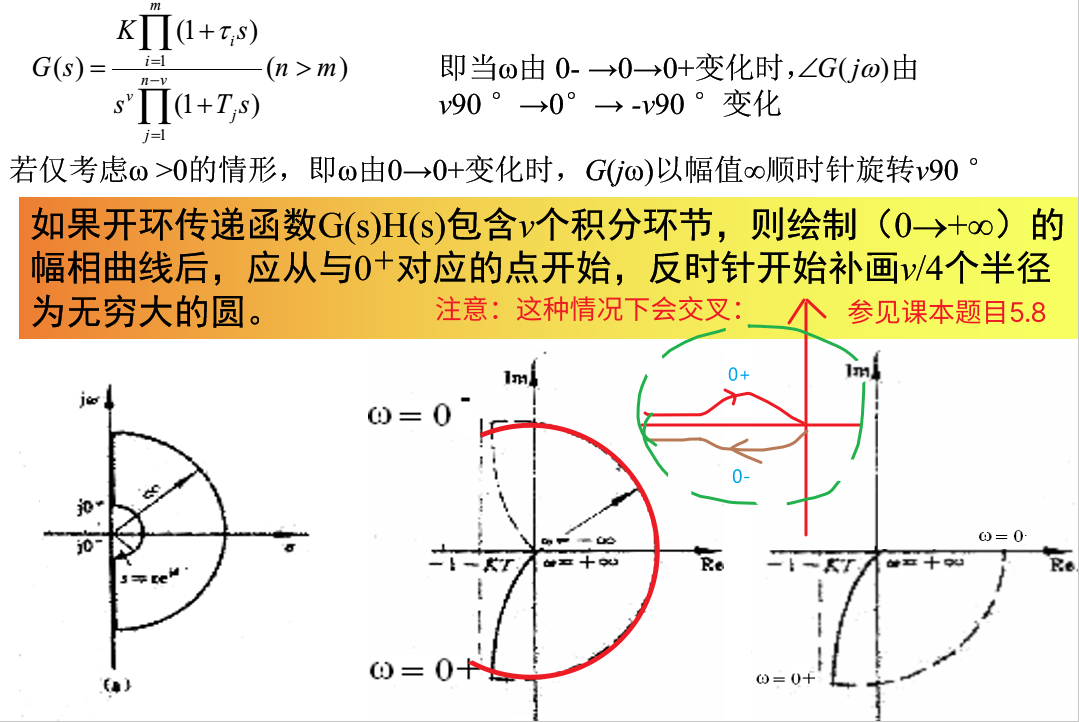
4. 技巧
要求“使用波特图“计算闭环系统稳定时的K值时,如果$G(j \omega) H(j \omega)$不好算,可以先用劳斯判据把结果算出来,再假装用波特图计算。
计算$\omega_c$时,学会使用分段计算
若某一段$\left[ \omega_1, \omega_2 \right]$的斜率为$k$(单位dB/dec),则$L\left(\omega_{2}\right)=L\left(\omega_{1}\right)-k\left(\lg \left(\omega_{2}\right)-\lg \left(\omega_{1}\right)\right)$
第五章 采样控制系统
信号的采样和恢复
z变换
脉冲传递函数
这一部分只要注意到有采样开关的环节需要先z变换后相乘,无采样开关的环节先相乘再z变换就可以了。剩下的就是背诵z变换公式这样的基础知识即可。
- 定义
- 开环系统
- 闭环系统
稳定性分析
稳态误差
第六章 状态空间分析与设计
状态空间模型
状态方程和输出方程
传递函数矩阵
预解矩阵$\Phi (s)$
其中$a d j(s I-A)$是伴随矩阵,详见维基百科上的介绍。
注意:求出代数余子式之后,将对应位置的的代数余子式转置排列才是伴随矩阵。线性代数中常用的记号为$A^{*}$。
传递函数矩阵$G(s)$
状态方程求解
- 频域法
- 时域法
系统的可控性与可观测性
- 稳定性
- 可控性,可控性阵$Q_c$
- 可观测性,可观测性阵$Q_o$
由传递函数$G(s)$写状态方程
- 可控标准型
- 可观标准型